收录:计算机数学故事
作者:YY同学Serendipity
绘图:勤奋的三塔同学🍊
简述
微分中值定理包括罗尔中值定理、拉格朗日中值定理和柯西中值定理,较多出现在证明题中,该知识点往往考察联想记忆以及灵活运用定理的能力,整体难度中。
一、罗尔(Rolle)中值定理
1. 定义
如果函数
满足以下三个条件:
1.在闭区间 上连续
2.在开区间 上可导
3.
则在内有一点 ,满足
2. 证明
如果
是常函数,则显然恒存在
如果不是常函数,假设在 处取到 ,则
因为 可导,即 所以得证
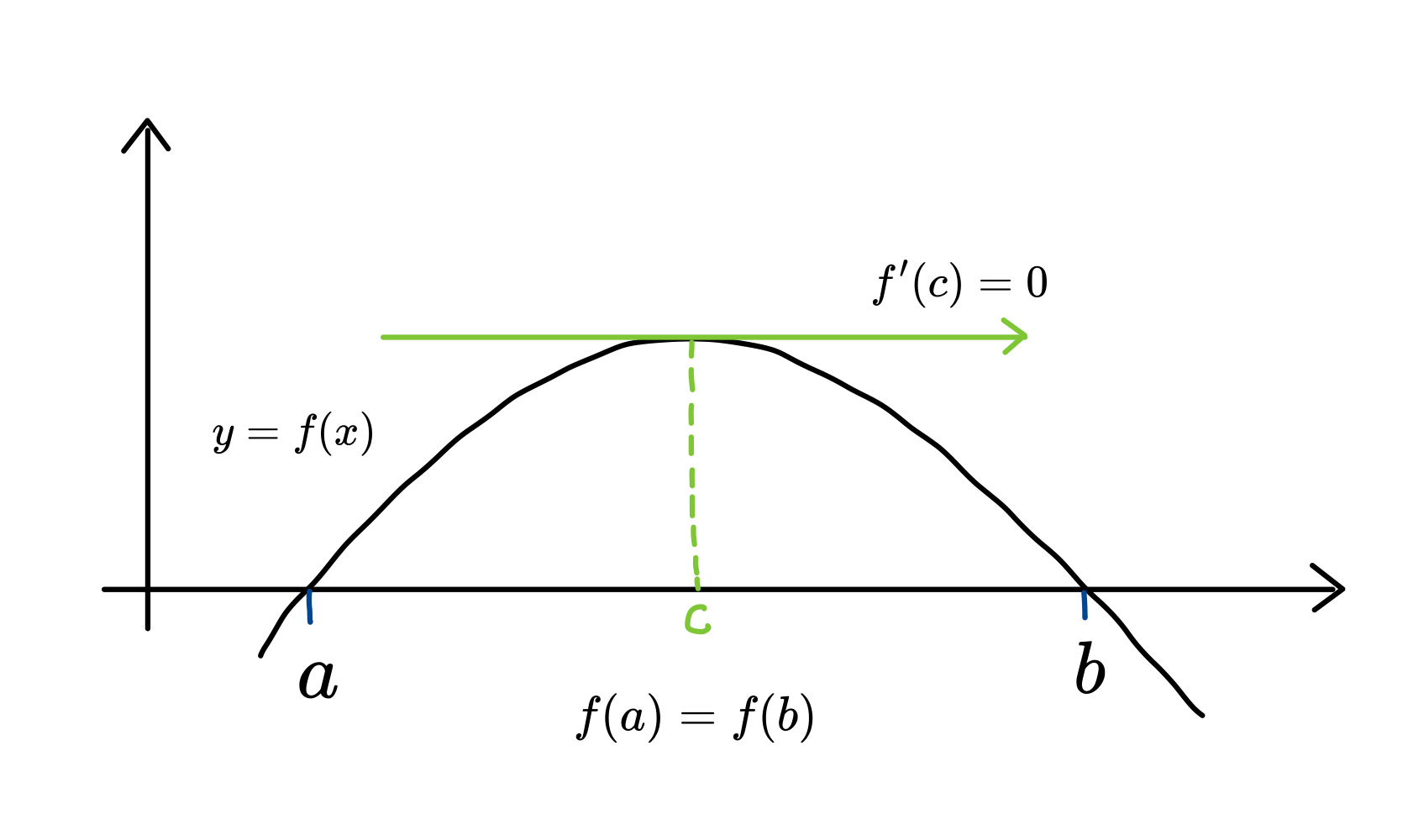
3. 几何意义
一定存在一条绿线(函数的切线)与
轴平行,如图:
二、拉格朗日(Lagrange)中值定理
1. 定义
如果函数
满足以下两个条件:
1.在闭区间 上连续
2.在开区间 上可导
则在内有一点 ,满足
2. 证明(采用函数构造法+罗尔定理)
我们先不急着证明,先观察定理的结论。我们会发现,如果将结论进行一下变形:
其结果是不是很像罗尔定理最后 的结论,因此我们需要构造函数 使 尽量与上式左边相同。我们将含有 的项当作自变量 然后积分找到 这样 然后考虑罗尔定理应用的条件是需要找到 因此当 时有 根据罗尔定理,则在 内有一点 ,满足 因此 变形之后即为拉格朗日中值定理的结论
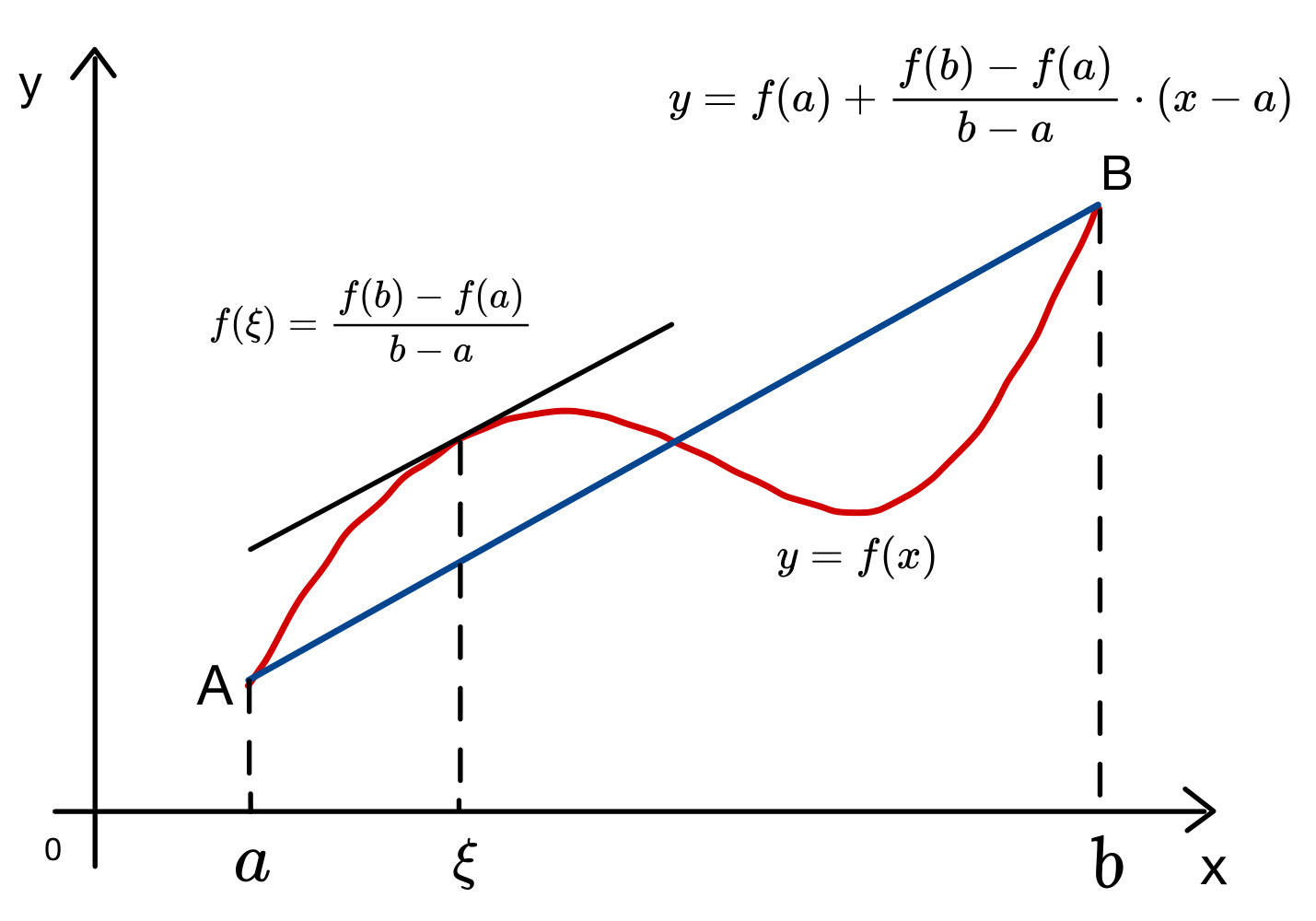
3. 几何意义
一定存在一条切线,它的斜率等于线
的斜率(即两线平行),如图:
三、柯西(Cauchy)中值定理
1. 定义
如果函数
满足以下两个条件:
1.在闭区间 上连续
2.在开区间 上可导且
则在内有一点 ,满足
2. 证明(采用函数构造法+罗尔定理)
同理,受拉格朗日中值定理证明的启发,我们先给原式做变形:
然后积分找到 当 时恰好有 所以根据罗尔定理有 变形之后即为柯西中值定理的结论,定理得证
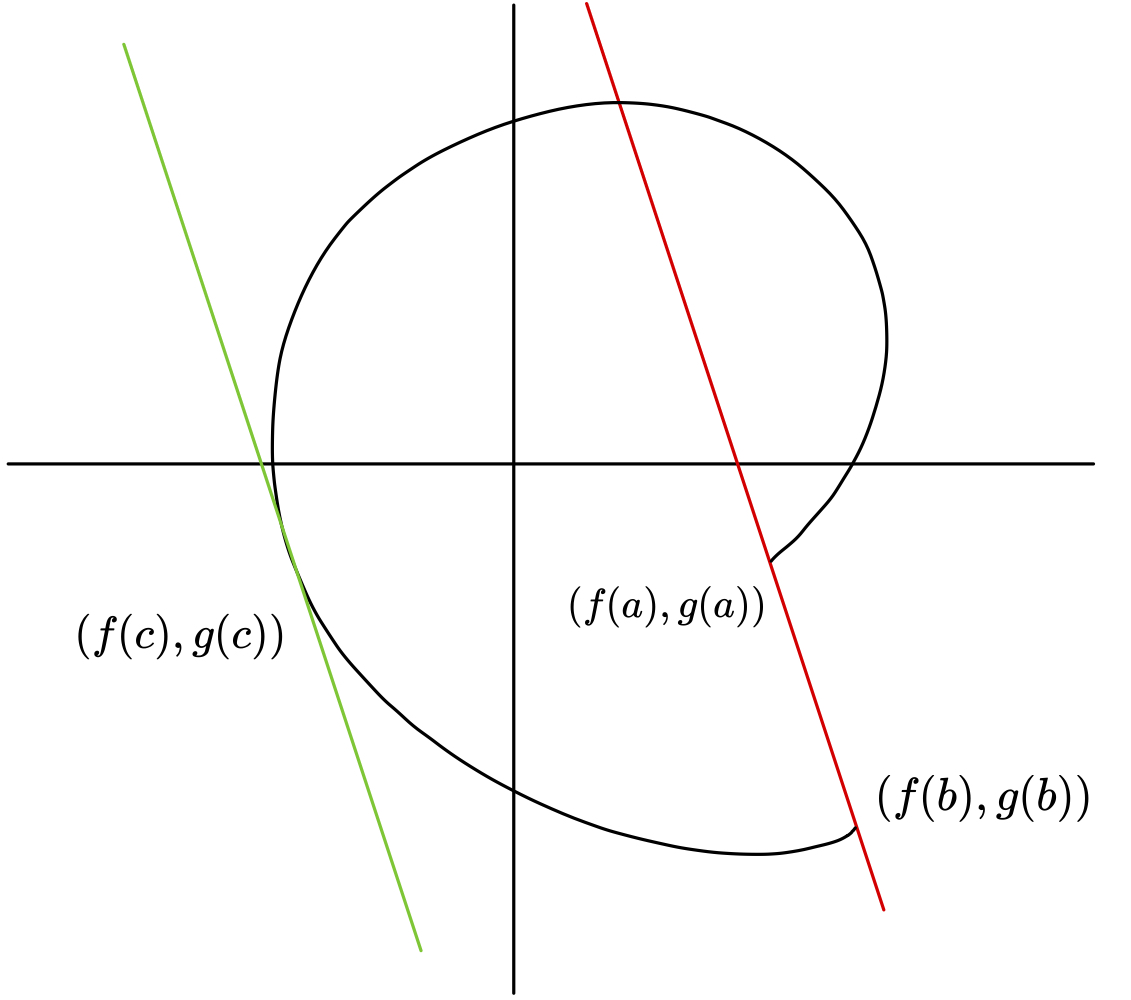
3. 几何意义
一定存在一条绿线(函数的切线)与红线平行,如图:
小结
可能细心的同学已经发现了,对于微分中值定理其实有:
即拉格朗日中值定理是柯西中值定理 时的特例,而罗尔中值定理也是拉格朗日中值定理 时的特例。从几何意义上讲,一定能找到与两个端点连线相平行的函数切线。这三个定理是从特殊情况推广到一般情况,如果理解了这些,相信大家也能很快地记住这三个非常重要的定理。